Struggles and Success with Network Flow: My Journey to Understanding the Ford-Fulkerson Algorithm

Published on November 2, 2024

In my recent algorithms class, I found myself facing a challenging topic: network flow. The topic was introduced in a lecture, and although I tried my best to keep up, I felt increasingly lost as we dove into the details. Concepts like "augmenting paths," "residual networks," and "flow capacity" swirled around in my mind, but I couldn’t quite grasp how they all fit together. It was frustrating, to say the least. 😩

The Challenge with Network Flow

Network flow problems involve finding the maximum flow in a network—a graph with nodes and directed edges, where each edge has a capacity that limits how much "flow" can pass through it. Although I understood the basic setup, the solution methods felt complex. One of the core methods we covered was the Ford-Fulkerson algorithm, which was supposed to help us find this maximum flow. Yet, despite our professor’s explanations, I was stuck. 🤯

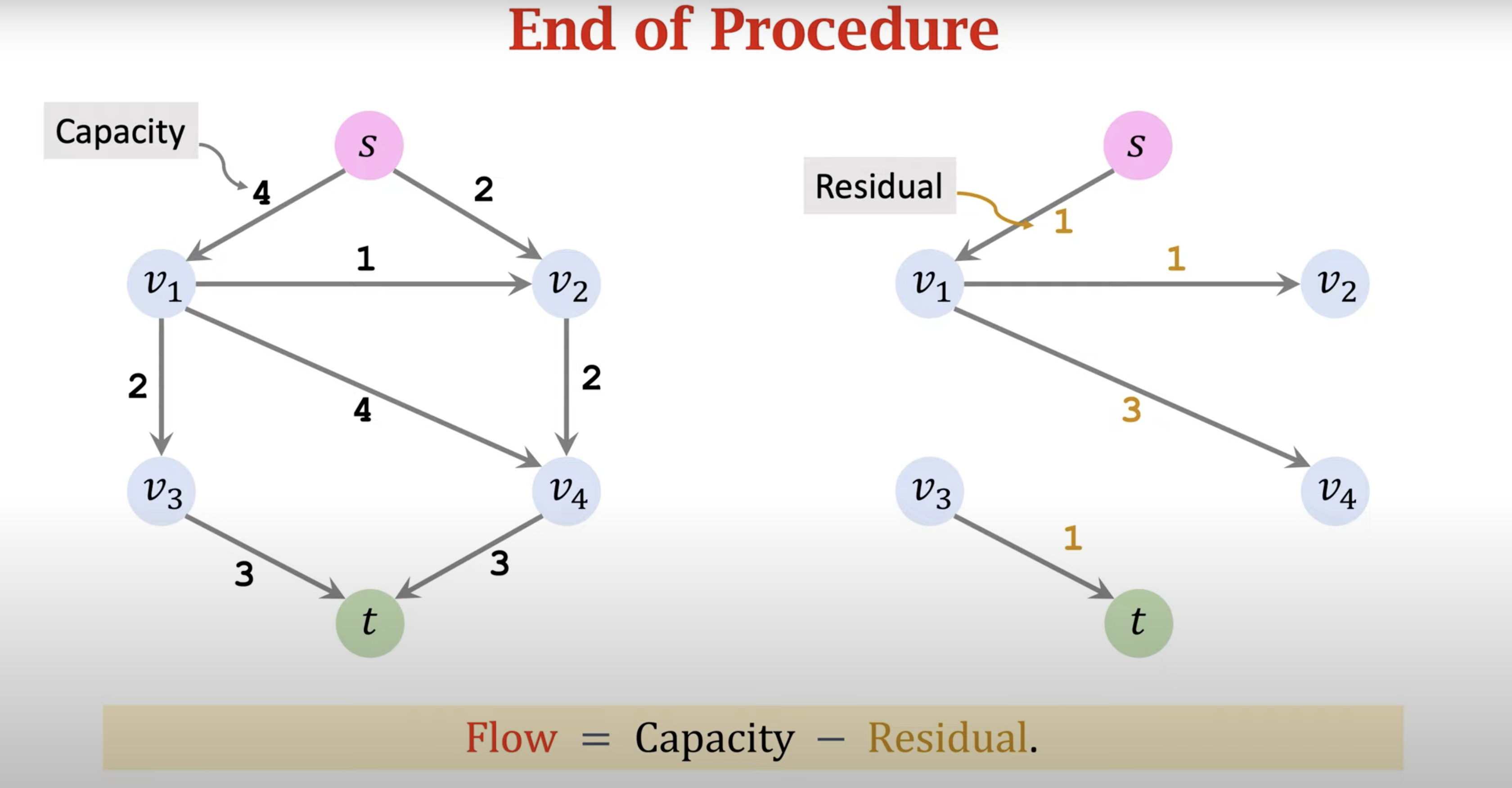
💡 Discovering the Ford-Fulkerson Algorithm

Determined to understand, I looked for additional resources and came across a helpful video in Mandarin that thoroughly explained the Ford-Fulkerson algorithm. This video linked here (it is only mandarin Chinese, but I think that you can auto-translate it in youtube) provided a visual breakdown that clarified the concepts of residual networks and augmenting paths, finally making the algorithm click for me. 🎉

Putting It All Together

After watching the video and practicing problems on my own, things finally started to make sense. I realized that the key was visualizing each step of the algorithm. By carefully following each augmenting path and updating the residual capacities, I could see how the network evolved, bringing me closer to the maximum flow.

Eventually, I managed to solve my first network flow problem from start to finish using Ford-Fulkerson, and it felt incredibly rewarding. 🏆 Reflecting on this process, I learned that sometimes concepts only make sense once you see them in action and work through the details.

Takeaways

This experience taught me that it’s okay to struggle with complex topics. The key is to keep trying, seek out helpful resources, and find explanations that make sense to you. Understanding Ford-Fulkerson and network flow wasn’t easy, but the process improved my problem-solving skills and gave me a greater appreciation for algorithms. 🚀